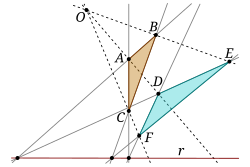
Uma ilustração do Teorema de Desargues, um resultado importante na geometria euclidiana e projetiva .
A Geometria (em grego antigo: γεωμετρία; geo- "terra", -metria "medida") é um ramo da matemática preocupado com questões de forma, tamanho e posição relativa de figuras e com as propriedades do espaço. Um matemático que trabalha no campo da geometria é chamado geômetra.
A geometria surgiu independentemente em várias culturas antigas como um conjunto de conhecimentos práticos sobre comprimento, área e volume, sendo que o aparecimento de elementos de uma ciência matemática formal é no mínimo tão antigo quanto Tales (6º século AC).
Por volta do 3º século AC a geometria foi posta em uma forma axiomática por Euclides, cujo tratamento, chamado de geometria euclidiana, estabeleceu um padrão que perdurou por séculos.[1] Arquimedes desenvolveu técnicas engenhosas para calcular áreas e volumes, antecipando em várias maneiras o moderno cálculo integral.
O campo da astronomia, especialmente o mapeamento das estrelas e planetas na esfera celestial e a descrição das relações entre os movimentos dos corpos celestiais, foi uma das mais importantes fontes de problemas geométricos durante os mil e quinhentos anos seguintes.
Tanto a geometria quanto a astronomia foram consideradas no mundo clássico parte do Quadrivium, um subgrupo das sete artes liberais cujo domínio era considerado essencial para o cidadão livre.

geometria esférica é um exemplo de geometria não-euclidiana. Ela tem aplicações práticas em navegação e astronomia.
A partir da experiência, ou, eventualmente, intuitivamente, as pessoas caracterizam o espaço por certas qualidades fundamentais, que são denominadas axiomas de geometria (como, por exemplo, os axiomas de Hilbert).
Esses axiomas não são provados, mas podem ser usados em conjunto com os conceitos matemáticos de ponto, linha reta, linha curva, superfície e sólido para chegar a conclusões lógicas, chamadas de teoremas.
A influência da geometria sobre as ciências físicas foi enorme. Como exemplo, quando o astrônomo Kepler mostrou que as relações entre as velocidades máximas e mínimas dos planetas, propriedades intrínsecas das órbitas, estavam em razões que eram harmônicas — relações musicais —, ele afirmou que essa era uma música que só podia ser percebida com os ouvidos da alma — a mente do geômetra.
Com a introdução do plano cartesiano, muitos problemas de outras áreas da matemática, como álgebra, puderam ser transformados em problemas de geometria, muitas vezes conduzindo à simplificação das soluções.



Nenhum comentário:
Postar um comentário